Blog

Am 1. August 2014, genau 6 Jahre vor dem Tag, an dem ich angefangen habe, diesen Post zu schreiben, habe ich mit meinen Eltern und einem kleineren Freundeskreis in Münster am Aasee gegrillt.

Dabei wurde feierlich eine Seite aus dem Fachartikel, der Grundlage für meine Masterarbeit im Fach Mathematik war, verbrannt, siehe Titelbild.

Das war nämlich gleichzeitig der Anlass, denn die Masterarbeit habe ich nämlich am Tag vorher eingereicht:

Ich bekomme zwar nicht häufig, aber doch regelmäßig die Frage gestellt, was mich denn an der Mathematik faszinieren würde.

Zugegeben, oft stellen Menschen diese Frage in einem weniger positiven Unterton. 🙂

Das ist gar nicht so leicht zu beantworten, zurück geht es aber auf meine Faszination für Zahlen schon im Kleinkindalter. Ich möchte jetzt nicht zu küchenpsychologisch daherkommen, aber Zahlen sind im Grunde genommen eine Spielwiese. Eine Welt, die man wie im Computerspiel nach und nach erkunden kann. Nur ohne dass man hierfür überhaupt einen Computer oder zumindest eine super Grafik benötigen würde!

Während ich als Kind auf die Pflege, auf Ärzte usw. wartete, hatte ich zum Spielen nur meinen Kopf. Das reicht für diese spezielle Spielwiese.

In späteren Jahren habe ich genau diesen auch benutzt, mir diverse schöne Dinge jenseits der Mathematik auszumalen, zum Glück verfüge ich über eine Fantasie und keine Sorge, so ein hoffnungsloser Nerd bin ich dann zum Glück doch nicht. 😎

In diesem wie auch im nächsten Post möchte ich euch darlegen, warum ich es bedauere, dass speziell das Kopfrechnen leider speziell in unseren Schulen solch eine sekundäre Rolle eingenommen hat und in der Regel anstatt auf Kreativität primär auf „Auswendiglernen“ reduziert wird.

Geständnis: Auswendiglernen fand ich immer schon doof. Für das kleine Einmaleins ergibt das Sinn, wie wir später sehen werden, aber darüber hinaus ist es demotivierend und vor allem unkreativ.

Disclaimer: Ich habe viele Probleme mit dem Mathematikunterricht an deutschen Schulen, von denen viele allerdings auch in unserem Schulsystem generell verwurzelt sind. Darum soll es in diesem Beitrag allerdings nicht gehen. Ich bin gerne bereit, mit einer Pädagogin oder einem Pädagogen über die Anwendbarkeit meiner Methoden auf den Schulunterricht zu diskutieren.

Für meinen Teil bin ich aber heilfroh, nicht um 8:00 Uhr morgens (alleine dafür schon *kotz*) eine Horde von Puber-Tieren bändigen und vor allem mit ihnen noch einen vorgesetzten Lehrplan durchkauen zu müssen, der vor allem zu diesem Zeitpunkt weder mich noch sie sonderlich faszinieren dürfte.

Liebe Lehrerinnen und Lehrer, ich stehe euch gerne auch virtuell helfend zur Seite wenn gewünscht, aber sorry, die Suppe löffelt ihr ohne mich aus.

Ich werde mich in diesem wie auch im nächsten Post auf die vier Grundrechenarten konzentrieren (heute auf drei und nächste Woche auf die vierte Grundrechenart). Selbstverständlich gibt es viel mehr zu entdecken, aber glaubt mir, dass die Grundrechenarten schon mehr als ausreichen, um selbst einen vernünftigen Einstieg in die höhere (oder besser gesagt die „interessante“) Mathematik und sogar in die Beweisführung zu finden, hierzu allerdings erst nächste Woche mehr.

Ich werde, nach dem Vorbild Mathologers, meine Erklärung in 7 „Level“ unterteilen, wobei heute nur 1-4 dran sein werden, der Blogpost wird leider trotzdem schon lang genug, hoffentlich zumindest zumindest für die Hälfte von euch verständlich. Im Ernst, das würde mich angesichts des Themas schon sehr schmeicheln!

„Mathologer“ ist der YouTube-Kanal von Prof. Burkhard Polster, der seit Jahrzehnten schon in Melbourne (Australien) unterrichtet. Seine Videos sind interessanter und komplexer als alles, was ich hier jemals schreiben werde, leider werde ich ihm grafisch und von der Anschaulichkeit seiner Erklärungen her absolut niemals das Wasser reichen können. Wenn man so sagen kann, er ist definitiv eines meiner Idole.

Level 1: Addition

Diese Debatte fand tatsächlich vor wenigen Wochen so auf Twitter statt.

Fand ich natürlich ganz spannend, um aber richtige Erkenntnisse über grundverschiedene Herangehensweisen etc. zu gelangen, hätte man meines Erachtens eine Beispielaufgabe nehmen müssen, die weit weniger Resonanz erfahren und weit mehr Menschen abgeschreckt hätte.

Ich sage doch, ich wäre ein grottenschlechter Lehrer. Da stehe ich zu.

All right, jetzt will ich die Frage aber doch mal ordentlich beantworten und nicht immer nörgeln:

und „zu viel“, also 70.
(genauer gesagt rechne ich hier immer modulo 10)

Das machen übrigens auch auf Twitter die meisten so. Selbst bei anscheinend komplizierteren Aufgaben ist das Verfahren zumindest für mich gleich:

und die hinteren Teile addieren sich zu „zu viel“, also korrigieren wir auf 7900 oder, anders gesagt, siebentausend neunhundert. Diesen Teil des Ergebnisses können wir jetzt schon mal laut anfangen auszusprechen! Währenddessen rechne ich noch im Hinterkopf:

Zunächst dürfte euch aufgefallen sein, dass ich, wie übrigens die meisten Menschen, „von vorne nach hinten“ addiere, obwohl die schriftliche Addition typischerweise andersherum vorgeht. Hierfür sehe ich jedoch zwei ganz praktische Gründe:

• Alltagsanwendungen. Wer beispielsweise im Supermarkt im Kopf Geldbeträge addiert, möchte nicht zuerst alle hinteren Stellen der Summe ausrechnen müssen, die ihn oder sie bei der Frage, ob der mitgebrachte 50€-Schein für die Einkäufe ausreicht, sowieso nicht weiterhelfen. Wir leben nun mal in einer Welt, in der uns die erste Stelle einer Zahl viel häufiger interessiert als die letzte (für die Experten: Wir bemessen rationale Zahlen in der Regel nach ihrer archimedischen Norm) und warum sollten wir uns ein Leben lang mühsam antrainieren, mit den hinteren und damit den am wenigsten wichtigen Stellen anzufangen?
• Sprachliche Gründe. Bei großen Zahlen werden im Deutschen die ersten Stellen auch sprachlich zuerst genannt. Ich kann aus jahrzehntelanger Erfahrung bezeugen, dass ihr Eindruck erweckt, wenn ihr schon schnell, also im obigen Beispiel während ihr eigentlich noch rechnet, anfangt, das Ergebnis aufzusagen. Und bei noch größeren Zahlen hat dies den Vorteil, dass man sich diese nicht einmal mehr merken muss, weil man sie ja bereits gesagt hat. Praktisch 🙂

Ebenso habt ihr vielleicht gemerkt, dass ich bei der komplizierteren Beispieladdition in Zweierblöcken vorgegangen bin. Geht schneller und man muss sich etwas weniger merken, außerdem gibt es hierfür einen sprachlichen Grund, der interessanterweise nichts mit Mathematik zu tun hat:

Deutsch ist eine unlogische Sprache. Darin werden mir bestimmt Horden ausländischer Schüler und Studenten beipflichten. Hier meine ich jedoch speziell, dass die deutsche Sprache vorsieht, die letzten beiden Stellen einer Zahl in umgekehrter Reihenfolge aufzusagen, also „achtundfünfzig“ anstatt „fifty-eight“, geschrieben wird die Zahl nämlich eher gemäß der englischen Reihenfolge: 58.

Fun-Fact am Rande: In der dänischen Sprache wird diese Zahl buchstäblich wie folgt ausgesprochen:

   

Kein Witz, siehe das folgende Video für einen Überblick über andere interessante Sprachen dieser Welt, Deutsch ist was die Kompliziertheit seiner Zahlwörter betrifft nur im Mittelfeld würde ich sagen:

Trotzdem gestehe ich, dass die Addition auch bei mir wahrscheinlich beim Kopfrechnen noch mit die meiste Zeit in Anspruch nimmt. Sie ist im Grunde schon zu einfach – so einfach, dass es für sie leider gar nicht viele nette Tricks gibt. Fühlt euch also ermutigt, weiter zu lesen, auch wenn ihr euch mit größeren Additionsaufgaben schwertun solltet. Mir geht es beizeiten noch heute ganz genau so.

Nein, keine Sorge Mama, keine der zufällig ausgewählten vierstelligen Zahlen in diesem Artikel entspricht meiner PIN oder sonst irgendwelchen relevanten privaten Informationen *g*

Level 2: Subtraktion

Subtraktion, oder anders ausgedrückt „Minusrechnen“, gibt es nicht. Fake News!

Nein, im Ernst: Subtraktion ist für tatsächlich keine eigenständige Grundrechenart, nur so etwas wie eine Addition „an der Fleischtheke im Supermarkt“. Beispiel gefällig? Könnt ihr haben:

   

Eigentlich ist dies nur eine Kurzschreibweise für , in Worten: Man nehme und addiere dazu das Gegenteil (für die Mathematiker unter uns: Das additive Inverse) von .

Wie ist diese historisch lange Zeit mysteriöse Zahl, dieses „Gegenteil von“ definiert? Ganz einfach: Es ist die Zahl, zu der ich noch addieren muss, um sie zu „neutralisieren“, sprich bei Null rauszukommen. Genau, wie, leider, auch Schulden bei der Bank definiert sind, wo die Zahl hinter dem Minuszeichen angibt, wie viel Geld ihr noch tilgen müsst, nur, um danach wieder bei Null zu stehen.

Wie ist also die obige Aufgabe wörtlich zu verstehen?

„Man nehme und addiere etwas hinzu. Wenn ich jetzt zusätzlich auch noch hinzu addiere, habe ich insgesamt gar nichts addiert, bleibe also bei stehen. Mit anderen Worten, rein sprachlich umformuliert: Wir suchen eine Zahl, die ich zu addieren muss, damit im Ergebnis rauskommt.“

Na super denkt ihr euch vielleicht, und wie findet man diese Zahl?

Da dürfte jeder seine eigene Methode besitzen, ich für meinen Teil führe blitzschnelle Selbstgespräche mit mir, als wäre ich an einer Fleischertheke und müsste „raten“, wie viel Hackfleisch ich benötige:

„Reicht das, wenn ich 100 dazu tue?“
„Nein, das macht in der Summe 586, Ziel von 625 verfehlt.“
„200?“
„Nein, 686 sind etwa 60 Gramm zu viel.“
„Also 140?“
„Das macht 626, Ziel haarknapp verfehlt, nur noch eines zu viel!“
„Also kriegen Sie eines weniger, 139 ist das Ergebnis. Danke und schönen Tag noch!“

Natürlich laufen Selbstgespräche extrem verkürzt ab und nicht immer mit jedem Schritt einzeln, aber so lässt es sich meines Erachtens gut veranschaulichen. Bin für Alternativvorschläge natürlich offen und interessiert! Nur klassische Subtraktion „von hinten nach vorne“, so wie wir es in der Grundschule gelernt haben, wirkt mir für die meisten Menschen unnötig kompliziert wenn ich ganz ehrlich bin. Andere Meinungen selbstverständlich erlaubt!

Level 3: Verdoppeln und Halbieren

Wie bitte? Ist das nicht Multiplikation für Arme?

Im nächsten Level wird deutlich, warum ich diesen beiden Operationen einen solch besonderen Wert beimesse.

Wie im letzten Kapitel angedeutet, gibt es für mich eigentlich nur zwei Grundrechenarten: Addition und Multiplikation. Diese können manchmal unabhängig voneinander betrachtet werden, jedoch es gibt ein Gesetz, das regelt, wie die beiden sich gegenüber einander zu verhalten haben:

Das Distributivgesetz. Auf Potthässlich, äh Deutsch meine ich, manchmal in den Schulen auch Verteilungsgesetz genannt.

Interessanter Name, den ich euch nicht näher erklären werde. Letztendlich lässt sich das Verhältnis von Addition und Multiplikation nämlich auch an einem einzigen Fakt zusammenfassen:

Die Operation Verdoppeln (ich bezeichne sie im Kopf meistens kurz mit dem Buchstaben V, einfach um im Kopf irgend einen Platzhalter für sie zu haben, das muss niemand übernehmen) lässt sich einerseits als Multiplikation mit 2 verstehen – andererseits jedoch als Addition einer Zahl zu sich selbst!

Unglaublich, aber dieser eine fast schon banale Fakt über das Verdoppeln ist im Prinzip eine gleichwertige Beschreibung für das Distributivgesetz. Dieser Fakt, oder wie wir sagen dieses Axiom, sorgt in großen Teilen dafür, dass die moderne Mathematik so funktioniert, wie sie es tut!

Zumindest das Verdoppeln reduziert sich hiermit nur auf Level 1: Addition.

und wieder zu viel, also .
, also lautet das Ergebnis .

Zugegeben, das Wissen, dass das Doppelte einer Zahl, die auf „67“ endet, zwangsläufig immer auf „34“ enden muss, habe ich dank Erfahrung. Es ist jedoch kein Akt, auch diesen Schritt eben schnell auszurechnen. Verdoppeln ist eine Aktion, die wir im Alltag, ja auch unterbewusst, sehr häufig erledigen!

Und das Halbieren? Ähnlich wie bei der Subtraktion können wir auch hier und wieder den Dialog an der Fleischtheke durchspielen:

„Hälfte von 534?
200 ist zu wenig, 300 zu viel, 250 zu wenig, 270 zu viel, 265 knapp zu wenig, 267 passt genau.“

Kleiner Tipp: Wenn ihr in großen Zahlen eine gerade Ziffer seht, dürft ihr die Zahl nach dieser „abschneiden“ und die einzelnen Teile halbieren!

„Hälfte von 4768?
Hälfte von 4 ist 2, Hälfte von 76 ist 38, Hälfte von 8 ist 4.
Zusammengefügt lautet das Ergebnis also 2384.“

Hier galt sicherlich für mich auch in einem gewissen Maße „Übung macht den Meister“. Aber ich verspreche euch, wer im Kopf einigermaßen bequem Zahlen verdoppelt und halbiert, dem steht für eine Multiplikation, von der er bislang ohne Taschenrechner nur zu träumen gewagt hat, eigentlich nichts mehr im Weg.

Naja, sagen wir fast. 😀

Level 4: Multiplikation

Holt euch noch schnell eine Tasse Tee oder natürlich ein Bier, jetzt wird’s spannend!

Ich hoffe, ich habe euch nicht zu viel versprochen lol.

Ich höre zur Entspannung jetzt auf jeden Fall zuerst mal etwas weniger kulturell anspruchsvolle Musik aus meiner Kindheit:

Jetzt aber los, lass uns zusammen multiplizieren, ich glaube, ich habe schon eine gute Beispielaufgabe für uns gefunden:

   

Der eine Faktor steckt bereits im Bandnamen und der andere ist mir bei dem Songtext einfach so spontan eingefallen, keine Ahnung wieso eigentlich. 😎

Puh. Wie gehen wir an so eine Aufgabe überhaupt heran?

Scherzbolde sagen jetzt bestimmt: Taschenrechner holen, ich nehme euch den Witz schon mal vorweg 😎

Mein erster Schritt ist immer, die Faktoren 2 und 5 zu eliminieren. Bei der 69 lässt sich hier leider nicht viel machen, aber die 182 ist eine gerade Zahl und gerade Zahlen tragen in erster Linie „unnötigen Ballast“ mit sich herum, also lasst uns halbieren!

   

Die 2 wird jetzt schön tief in mein Unterbewusstsein weggesperrt, sie ist ab jetzt nicht mehr Teil der eigentlichen Aufgabe, sie soll uns nur noch daran erinnern, dass wir ganz am Ende einmal verdoppeln müssen!

Es bleibt also die Aufgabe . Hierfür gibt es viele schöne Rechenwege, manche funktionieren bei manchen Beispielen besser als andere, ich möchte euch hier eine sehr schöne Standardmethode vorstellen:

Rechtecke zurechtsägen!

Und hierfür brauchen wir noch nicht einmal Werkzeug und Schutzausrüstung!

Was tun, wenn wir zwei Zahlen haben, die wir nicht ohne weiteres miteinander multiplizieren können? Wir manipulieren sie!

Was passiert, wenn wir den einen Faktor ein bisschen größer und dafür als Kompensation den anderen Faktor ein bisschen kleiner machen?

Kann man sich vorstellen, als würden wir eine rechteckige Holzplatte mit den Maßen und vor uns haben, das Produkt, dass wir ausrechnen wollen, entspricht dann genau der Fläche, also der Menge an Holz die wir haben.

Diese Menge ändert sich aber garantiert nicht, wenn wir einen kleinen Streifen von rechts absägen und ihn wie im Bild oben wieder anfügen:

Unsere Holzplatte sieht am Ende dann genau so aus:

Was heißt das jetzt?

Wir dürfen die beiden Faktoren und „aufeinander zubewegen“ – Also zum Beispiel ersetzen durch oder auch durch – und das einzige, das wir bei dieser Aktion „hinzuschummeln“, ist das kleine Rechteck in der oberen rechten Ecke. Hierbei ist offensichtlich das kleine Stück, dass wir ursprünglich abgesägt haben und das Stück, dass wir noch zusätzlich hätten absägen müssen, damit die beiden Seiten gleich wären.

Lasst uns die Faktoren und manipulieren und aufeinander zubewegen, und der offensichtliche Kandidat hierfür ist .

Hierfür haben wir beide Faktoren nur um 1 korrigiert. Damit aus den der andere Faktor von geworden wäre, wäre noch eine weitere Korrektur um 21 nötig gewesen (eine Korrektur, die wir aber nicht machen wollen!).

Das kleine Rechteck, welches wir dadurch, dass wir durch die deutlich freundlichere Aufgabe ersetzt haben, „hinzugeschummelt“ haben, hat also die Ausmaße 1 und 21. Dieses „hinzugeschummelte“ Rechteck können wir leicht ausrechnen, es hat die Fläche .

Unsere eigentliche Multiplikation besteht nun nur noch in der Rechnung . Die beiden Nullen am Ende lassen sich zunächst ignorieren und später wieder anfügen, also rechnen wir und – tadaa, wir haben es geschafft, unsere komplizierte Multiplikationsaufgabe auf eine Aufgabe aus dem kleinen Einmaleins zu reduzieren!

Die eigentliche Rechnung läuft jetzt wie folgt ab:

• , Grundschule lässt grüßen!
• Jetzt müssen unsere beiden geparkten Nullen aus der Aufgabe wieder angefügt werden, also verbessern wir unser Ergebnis auf .
• Denkt daran, beim Sägen haben wir ein kleines Rechteck mit der Fläche hinzugeschummelt, das müssen wir jetzt ehrlicherweise wieder abziehen! Für die Subtraktion siehe Level 2, wir korrigieren hiermit unser Zwischenergebnis auf .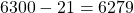
• Sind wir jetzt fertig? Leider noch nicht! Ganz am Anfang haben wir einmal den Faktor 2 abgespalten und jetzt ist der böse auf uns, dass wir ihn so lange ignoriert haben. Um das wieder gutzumachen, müssen wir jetzt zum Abschluss noch einmal verdoppeln. 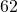ergibt verdoppelt , ergibt verdoppelt jedoch garantiert einen Überlauf für die letzten beiden Stellen, also korrigieren wir die ersten Stellen auf .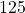
• verdoppelt gibt auf den letzten beiden Stellen – wenn du das nicht sofort siehst, darfst du dich auch erinnern, dass die entstanden ist, in dem wir das kleine Rechteck von abgezogen haben und für die Verdoppelung dieses einfach noch mal abziehen! liefert das gleiche Ergebnis.

Wir haben für das Endergebnis also vorne eine und hinten eine , ergibt zusammengefügt 12.558.

Zugegeben, ich weiß jetzt selber nicht, wie anschaulich das Beispiel gewesen ist. 😀 vielleicht in stark verkürzter Fassung nochmal anhand einer anderen Multiplikation:

   

• Der eine Faktor 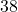ist offensichtlich gerade, der andere durch 5 teilbar. Eine sehr schöne Kombination, denn hiermit können wir beide Faktoren vergessen und müssen am Ende lediglich noch eine Null anhängen.
• und , Letzteres ist beispielsweise abermals durch Verdopplung auszurechnen. wir rechnen jetzt also .
• Durch den „Sägetrick“ verbessern wir auf , hierdurch wird ein kleines Rechteck der Größe hinzugeschummelt, das wir gleich wieder abziehen müssen natürlich!
• Zwei Nullen abspalten, es bleibt das Produkt .
• Jetzt erfolgt die eigentliche Multiplikation: . 😎
• Zwei Nullen wieder anfügen:
• Geschummeltes Rechteck wieder abziehen:
• Jetzt müssten wir noch einmal verdoppeln und noch einmal mit 5 multiplizieren, die Aktionen zusammen heben sich jedoch mehr oder weniger gegenseitig auf, am Ende müssen wir nur noch eine Null anhängen: 5890.

Wer dieses Programm (zugegebenermaßen manchmal garniert mit noch ein paar anderen Tricks, die ich euch heute erspare) regelmäßig innerhalb von wenigen Sekunden im Kopf abspult, hat danach in der Schulklasse nicht unbedingt mehr viele Freunde übrig. Ich hab’s für euch getestet 😉

Zwei Hinweise, die ich euch zum Abschluss geben möchte: Multiplikation und Division mit 5 vertauscht im Prinzip nur die Rollen von „verdoppeln“ und „halbieren“ mit einer kleinen Korrektur zum Schluss:

• Multiplikation mit 5 ist Null hinten anhängen und anschließend halbieren.
• Division durch 5 ist verdoppeln und anschließend eine Null von hinten „killen“.

Gewissermaßen betrachte ich die Faktoren 2 und 5, für die Naturwissenschaftler unter uns, so ein bisschen wie Säuren und Basen in der Chemie. Wir extrahieren sie aus den Lösungen, bevor wir diese zusammenmischen und geben sie nachträglich wieder hinzu. Wobei es wie in der letzten Beispielrechnung passieren kann, dass die Säure und die Base sich gegenseitig neutralisieren und wir am Ende nur noch harmloses Salzwasser, für uns Mathematiker eine Null am Ende, hinzufügen müssen.

Übrigens: Für den Fall, dass das kleine „geschummelte“ Rechteck in der letzten Skizze ein Quadrat ist, spricht man auch von der 3. Binomischen Formel (wobei „Sägetrick“ oder „Rechteck-wird-Quadrat-Formel“ für mich nach wie vor anschaulicher und besser vorzustellen ist). Manchmal, wenn ich auch mit dem Sägetrick nicht mehr weiter weiß, säge ich einfach so, dass sowohl das große als auch das kleine Rechteck zu Quadraten werden und benutze, dass ich die meisten Quadratzahlen schon auswendig kenne, aber das ist endgültig Nerdstuff. 😎

Kleiner Teaser zum Schluss: Nächstes Mal führen wir einen mathematischen Beweis mithilfe unseres besten Freundes und treuesten Begleiters – ja, ihr habt richtig gelesen: Ein Hund (und der Mann bzw. die Frau, mit der er spazieren geht) werden beim nächsten Mal den Beweis für uns liefern!

Ach Vinci, du fehlst mir sehr! <3